Annuity Calculator
The Annuity Calculator on this page is based on the time-value-of-money or "finance theory" definition of annuity. By that definition, an annuity is a series of fixed payments over a certain amount of time. This annuity calculator was not designed to analyze an Insurance Annuity which can mean something entirely different from the finance theory definition.
Because of the general definition of annuity, an Annuity Calculator might calculate the future value of a savings investment plan (as many online annuity calculators do). I've already created a few savings calculators, so instead, I created the following Annuity Calculator to answer general questions related to taking a withdrawal or annuity payment from a fixed-rate savings account. Example questions might be:
- What is the withdrawal or annuity payment per year over n years if I start with $P?
- What do I need to have saved for retirement in order to withdraw $A per year for n years?
- How many years can I withdraw $A if I start with $P?
Each of these questions is very easy to solve for using built-in Excel formulas, which I will explain in detail below. Or, you can just dive into the Annuity Calculator right now. Try the Savings Calculator if you are looking for a way to determine how much you will have saved by age 65 by making regular contributions.
Also, to figure out whether the initial payout (the first annual payment after you retire) is sufficient, you may want to use the Inflation Calculator to compare what you think you could live on based on today's prices to what you may need the first year of your retirement.
Annuity Calculator
for Excel and OpenOffice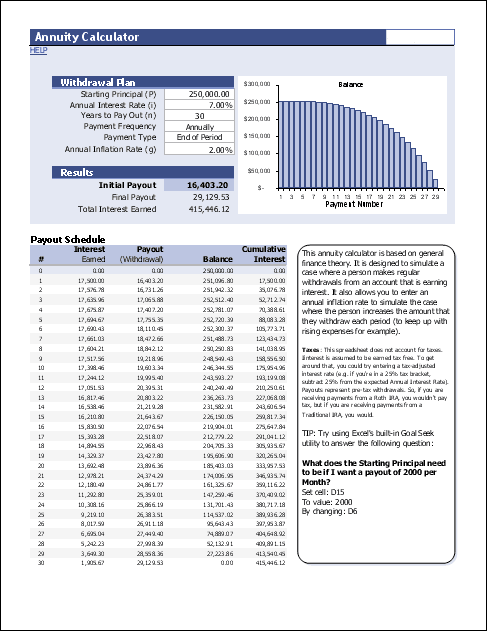
Description
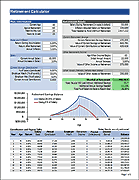
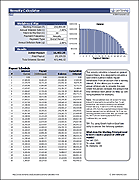
This Annuity Calculator spreadsheet contains two worksheets.
The first worksheet shows a yearly cash flow table and a graph of the balance. It solves for the annuity payment amount.
In the second worksheet shown in the screenshot on the left, you can solve for the annuity payment, the initial principal, or the number of years to pay out.
Both worksheets allow you to specify an annual inflation rate which will cause the withdrawal or annuity payment to increase over time.
Annuity Calculator Formulas
As a financial term used for time-value of money calculations, an annuity is the name given to the uniform series cash flow. It is represented as a payment of amount A starting at t=1 and remaining constant through t=n, as shown in the cash flow diagram in figure 1 below.
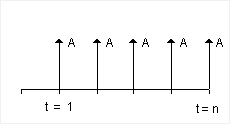
Fig 1. Uniform Series or Annuity Cash Flow (the same payment amount A from t=1 to t=n)
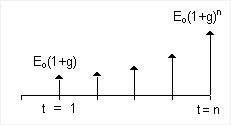
Fig 2. Exponential Gradient Series Cash Flow (g might be the inflation rate for example)
The annuity represented in figure 1 is called an Ordinary Annuity, or an annuity in which the payments are made at the end of each period. Monthly mortgage payments are an example of an ordinary annuity. An Annuity Due (see Fig 3) is one in which the payments are made at the beginning of each period. Examples of annuities due might be deposits in savings, retirement withdrawals, rent payments, or insurance premiums.
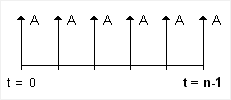
Fig 3. Cash flow diagram for an Annuity Due
The Excel functions PMT, PV, FV, and NPER can handle both types of annuities. These functions are all inter-related, based on the equivalency formula below, where type is used to identify the type of annuity (0 for an ordinary annuity or 1 for an annuity due).
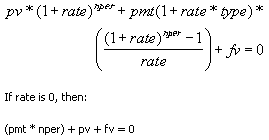
Fig 4. From the Excel Help documentation for the PV function
An inflation-adjusted annuity payment, something you might want to consider for retirement withdrawals, would actually be termed an exponential gradient series in finance theory. The cash-flow diagram for the exponential gradient series is shown in Figure 2.
Annuity Calculator Formulas
The formulas for solving for the annuity payment, annuity payout period, and initial savings are listed below. You can consult the following table for the definitions of the variables used in the equations.
| Variables | |
|---|---|
| P | Initial Principal |
| A | Annuity Amount |
| Eo | Exponential Gradient Amount |
| n | Number of annual Annuity Payments |
| i | Annual Interest Rate (effective rate) |
| g | Annual Inflation Rate |
| type | 0 = Ordinary Annuity (Payments at end of period) 1 = Annuity Due (Payments at beginning of period) |
Solving for Annual Annuity Payment Amount
A =PMT( i, n, -P, 0, type)
Solving for Starting Principal (Present Value of an Annuity)
P =PV( i, n, -A, 0, type)
Solving for Years to Pay Out
n =NPER( i, -A, P, 0, type)
Adjusting the Annuity Payment for Inflation
The Annuity Calculator was designed for use as a retirement calculator, where withdrawals are made each year. A very basic fixed-annuity calculator assumes the withdrawals are constant for n years. However, the reality is that the withdrawal amount will most likely need to increase each year due to inflation.
Don't get the inflation adjustment of the withdrawal amount mixed up with the terms variable annuity or adjustable annuity. These terms usually apply to the interest rate and are typically used to describe Insurance Annuities.
Without going through the derivation, suffice it to say that to use the PV, FV, PMT, and NPER formulas above for an inflation adjusted annuity payment, or more accurately an exponential gradient series, you substitute the variable Eo for A and z-1 for the annual interest rate where
z = (1+i)/(1+g)
Example: Solving for the Initial Value, Eo
For the inflation-adjusted calculations in the Annuity Calculator, the annual payment that is calculated using the PMT function is the value Eo (see the cash flow diagram in Figure 2 for clarification). If type=1 (Payments at Beginning of Period), Eo represents the first annual payment. However, if type=0, the first annual payment is Eo*(1+g).
Eo =PMT( (1+i)/(1+g)-1, n, -P, 0, type)
To calculate the inflation-adjusted payment for year j, you can use the FV formula:
Eo*(1+g)j =FV(g,j,,-Eo)
Insurance Annuities
As I mentioned at the start of this page, an Insurance Annuity is not necessarily the same thing as the type of annuity I've discussed above. For example, if you were to purchase a 5-year Deferred Fixed Annuity, you might receive your payment as one lump sum at year 5. Clearly, that is not the same thing as the finance theory definition of annuity. Perhaps more subtle, an Immediate Fixed Annuity might calculate your monthly payment for a 5-year 6% annuity by first calculating the future value as FV(6%,5,0,-100000) and then dividing by 5*12=60 to give $2,230.38 per month. That is NOT the same as using PMT(6%/12,5*12,-P)=$1,933.28.